来源:科学人微信公众号

大城市的交通,从来都不让人省心。多年的“逆来顺受”,我们已经能坦然面对早、晚高峰这种可以预料的堵车。但是那些突如其来的堵车还是让人抓狂:有时车辆不多、车道平整,既无事故发生也没停顿车辆,车流速度却突然降了下来,甚至整片交通都陷于停滞。往往正是这样的堵车导致你约会迟到。
这种莫名奇妙的堵塞现象被交通专家称为“幽灵堵车”(Phantom Traffic Jams)。为了找出原因,数学工作者们提出了许多的模型,直到物理学家们伸出了援助之手,他们最终找到了答案。故事,让我们从头说起。
早先的研究:跟车模型
交通堵塞是伴随着福特 T 型车出现的。当福特公司采用了现代流水线的生产方式后,汽车的生产效率得到了极大的提高,随之而来的汽车迅速普及也导致了交通状况的恶化。堵车问题一出来就吸引了数学家们的目光,在当时还方兴未艾的系统论和控制论似乎在这个问题上展现了自己的用武之地。为了应用自动控制理论,首先要分析作为车流最小单元的单个车辆的行为。 1950 年,罗伯特?赫尔曼博士基于动力学方法提出了跟车理论,随后到 1953 年学者 Reuschel 和 Pipes 提出完整的数学模型。这一理论的核心内容是驾驶员总倾向于与前方的车辆保持一定的距离,当前方的车辆加速时他会加速跟上,而如果前方的车辆突然减速他也会一同减速以免发生碰撞。但是驾驶员还存在着一定的反应时间T,据此研究人员认为在 t T 时刻后车的加速度将是 t 时刻两车速度、距离差的函数:
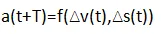 这一理论常用的模型是:
这一理论常用的模型是: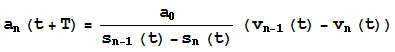 虽然这一模型在理论上是合理的,同时数学结构也足够完整,但是由于缺乏足够的实验支撑,它在很长一段时间内都被学界质疑。
虽然这一模型在理论上是合理的,同时数学结构也足够完整,但是由于缺乏足够的实验支撑,它在很长一段时间内都被学界质疑。也许是觉得自己对交通堵塞也负有一定的责任,随后不久,美国通用汽车公司实验室开始对人们在驾车时的行为展开了研究。当时的实验室负责人拉里?霍夫斯塔德请来了赫尔曼博士主持对跟车模型的进一步研究。为了说明这一理论的正确性,物理学家们利用通用汽车公司的优势在试车场搭建了一条环形实验公路进行车流的模拟实验。他们把前车的后保险杠和后车的保险杠用细线连起来,通过后车上携带的轮轴计算两车之间距离,并找来不同的司机进行测试。最终实验结果证明后车的加速度确实与前后车之间的相对速度有很强的相关性,这种关系里还有 1 秒钟左右的时间滞后和一个“获得性因子”,该因子似乎取决于车辆之间的距离。这一结果最终发表在了 1958 年的《运筹学报》上,从此“跟车模型”得到认可。
用流体类比交通状况
但问题还远远没有解决。虽然跟车模型模拟了司机的行为,却无法告诉我们整体的交通状况是怎样的。不过物理学家们注意到,跟车模型中车辆的行为与液体中分子的行为类似,这时自动控制理论让位给了统计物理。1955年,英国学者莱特希尔和惠特曼受跟车模型的启发,将交通流视为由单个“车分子”组成的某种流体,并与实际流体相比较,可以有下面的类比:
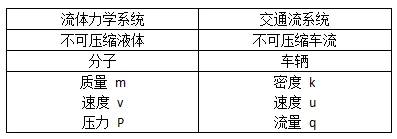 所以仿照实际流体可以建立以下方程:
所以仿照实际流体可以建立以下方程:(1)状态方程

(2)连续性方程
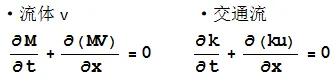
(3)运动方程

如此一来,车流密度的忽高忽低就可以类比为水面的波动。不过在当时,这个理论与实际数据吻合的并不好,这是由于交通流与实际流体仍有一些差别。比如说这一模型没有考虑到速度与惯性的影响。同时这些方程适用的条件是流体处于平衡态,当道路上的车辆不多的时候这一假设还没有什么问题,但当处于交通高峰期的时候(这恰恰是我们经常要分析的情况),这一假设就不太适用了。而且速度与密度的关系也并不像之前假设的那样。但是这一模型最早提出了用流体模型来模拟交通流的思路,从此“车流”不再仅仅只是个比喻,而是实实在在的数学模型。
“爆炸波”模拟交通堵塞
在此之后,车辆的交通流模型又经过了许多次的改进。例如引入高阶连续条件以计算速度与惯性的影响,或是引入液体中的音速与粘度系数等参数,不是把车流比拟为水流,而是把车流比拟为粘稠的蜂蜜或者焦油。2012年,又有一项研究成果就与堵塞的产生与传播有关。来自 MIT 的一个研究小组发现,与惯常所认为的堵塞往往是由某个司机的错误操作引起的不同,即使所有的司机都没有犯错堵塞仍然会产生,这也正是幽灵堵车的原因。由于不同车辆的速度之间往往存在着细小的差别,而这些差别会积累并在某处形成一个车流密度的极大点。他们把超过一定阈值的极大点称为“堵塞子”。这个“堵塞子”移动的速度比车流略慢,而且不会自行消失。这样堵塞就会在队列中传播并逐渐积累,最终发生车流密度的跳变形成一个波峰,所谓的“堵塞波”就这样产生了。下面这个视频就形象地说明了这个过程。通过计算他们发现,这个“堵塞波”的传播方式与爆炸产生的震波非常相似,而它的行为也可以通过某些波动方程加以预测。
实际上,这个理论已经可以应用到实际交通的控制中。采用一种被称作“绿波”的交通模式引导交通可以有效解决文章开头提到的“幽灵堵车”,这一方法的思路是既然车流的密度是像水波那样波动的,那么只要对每一个波包,当其到达路口时给他们绿灯,当高峰通过后再放行其他方向的车辆。这样总体的等待时间就得到了优化。同时这样也对车辆的速度进行了控制,高于平均速度的车辆将被迫等待,而低于平均速度的车辆则会努力赶上波峰。交通流理论是将物理学现有模型应用于跨领域情况的一次成功尝试。随着对这方面研究的深入,也许彻底解决交通拥堵问题的答案就蕴藏其中。
参考资料:
[1] Denos C。 Gazis。交通理论的创立。运筹学报,2002(作者是早期通用交通流模型研究小组的成员之一,本文是Operations Research第50卷第1期纪念该杂志发行五十周年的特稿中的一篇,记录了交通流理论早期开拓者的研究经历)
[2] 吴正,低速混合型城市交通的流体力学模型。力学学报,1994
[3] Traffic Modeling - Phantom Traffic Jams and Traveling Jamitons
