质数又叫素数,只能被1和自身整除,是所有大于1数字的基本组成。也就是说,每个数字要么本身就是一个质数,如2、17、53或673,要么就是质数的乘积,如17119(17 x 19?3)。
此外,每个数字都只有一种方法可以分解成质数。这不仅仅只是个猜测:在1801年,德国著名数学家卡尔·高斯(Carl Gauss)给这个“算术基本定理”作出了证明(虽然似乎古希腊数学家欧几里得在2000年前可能就已作出证明)。

除了它们的基本性质,质数看似正确但却无法证明的性质吊足了数学家的胃口。
例如,欧几里得提出提出了一种巧妙的方法来简单证明了质数有无限多个,但直到今天还没有人能证明有无穷多个“素数对”,如5和7或59和61, 其中两个连续的奇数是素数。
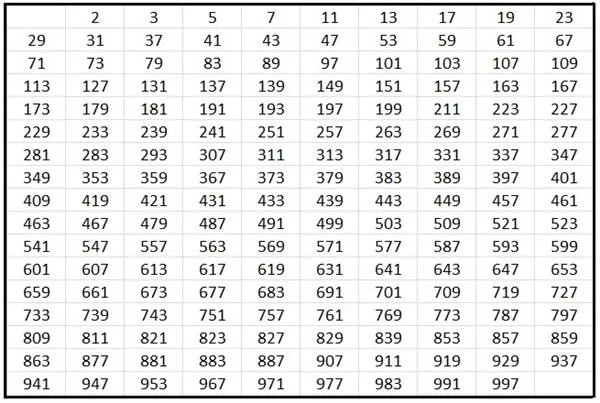
1到1000之间的质数
然后在1742年首次提出了哥德巴赫猜想(Goldbach's Conjecture)——任意一个大于5的整数都是三个质数之和。
再次,虽然这个命题被广泛认为是正确的,但时至今日仍没有人成功地证明了哥德巴赫猜想。
数字、比赛和消遣
证明给定一个数字是质数长久以来已被用于证明计算能力。最初都是被“专家”用于表演心算的天赋,后来被用于测试电子计算机的计算能力。
目前,已知最大的质数为2^(74,207,281)-1。它由互联网梅森质数大搜索(Great Internet Mersenne Prime Search)于2016年发现,该质数拥有22,338,618位数字。

自20世纪70年代末以来,质数已经具有巨大的商业意义,因为它们构成了RSA加密算法的核心,被广泛用于金融交易的保护。
粗略来讲,RSA加密系统基于这样的事实:没有快速的方法能将一个很大的数分解成两个类似大小的质数,因此可以将两个大数的乘积公开作为加密密钥。
虽然许多人认为这是真的,但仍然缺乏坚实的证据。鉴于利害关系,这也许会令人很不安——因为这相当于一个银行宣称肯定没有人会找到底下放有安全钥匙的垫子。
